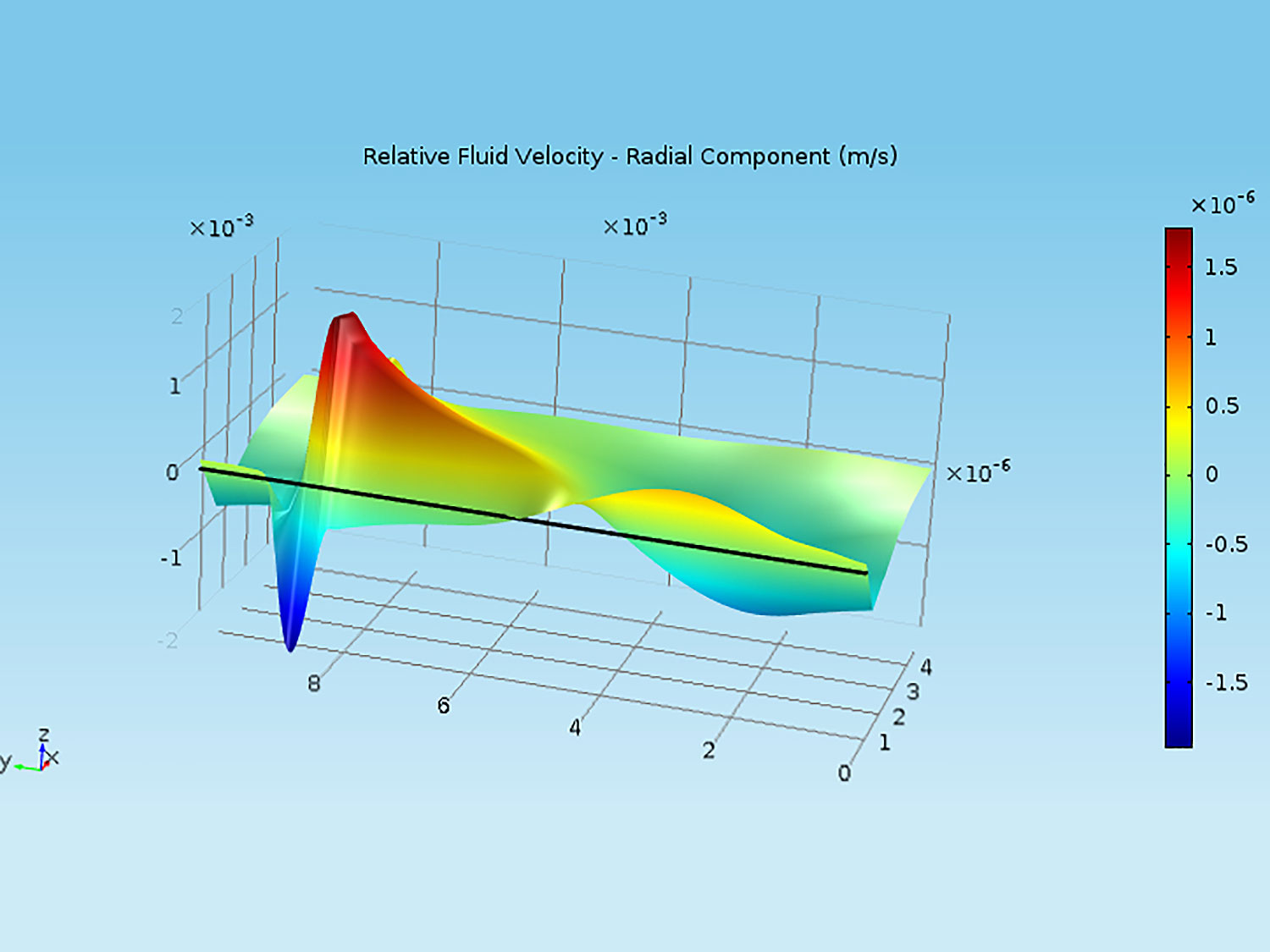
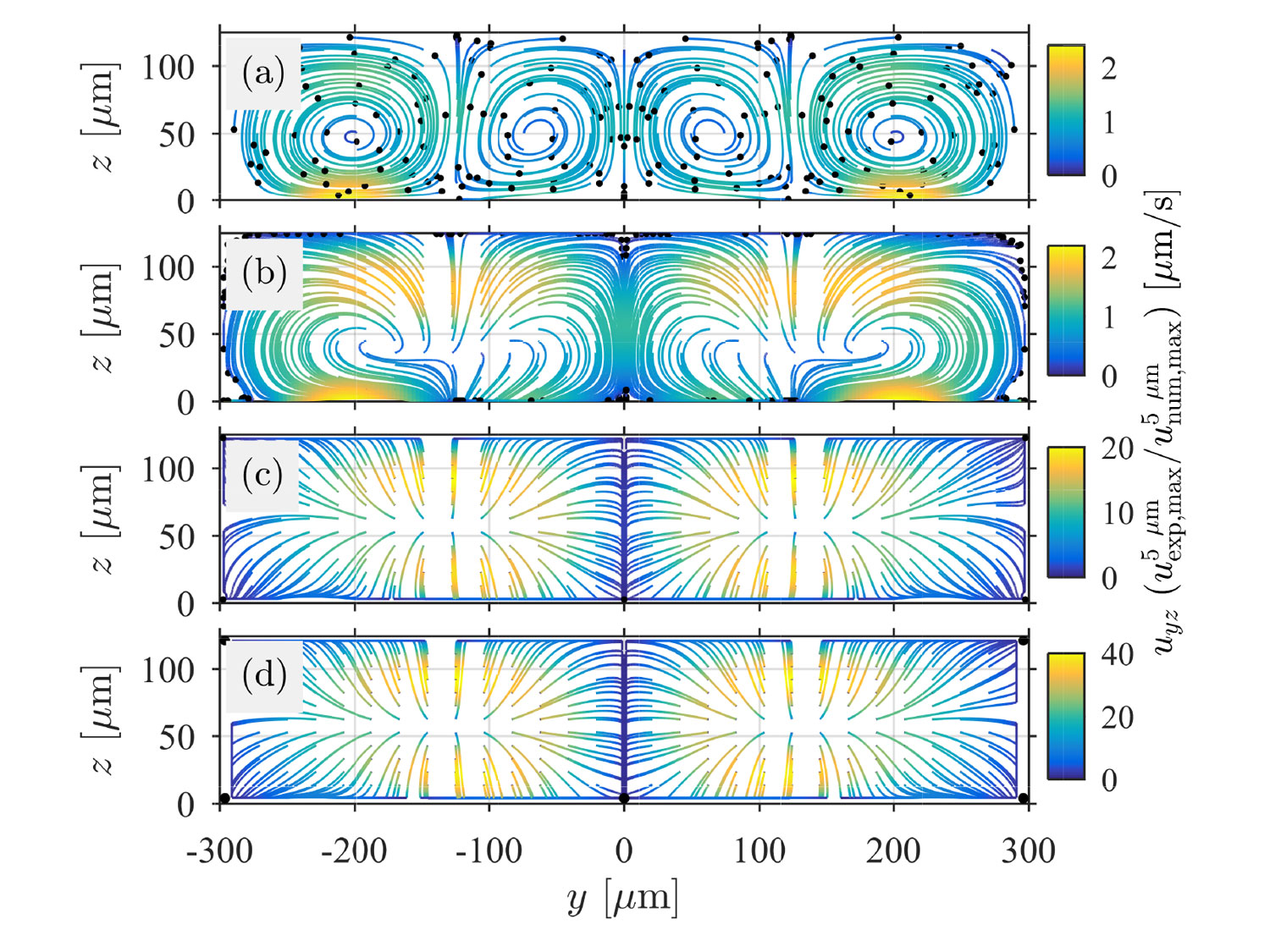
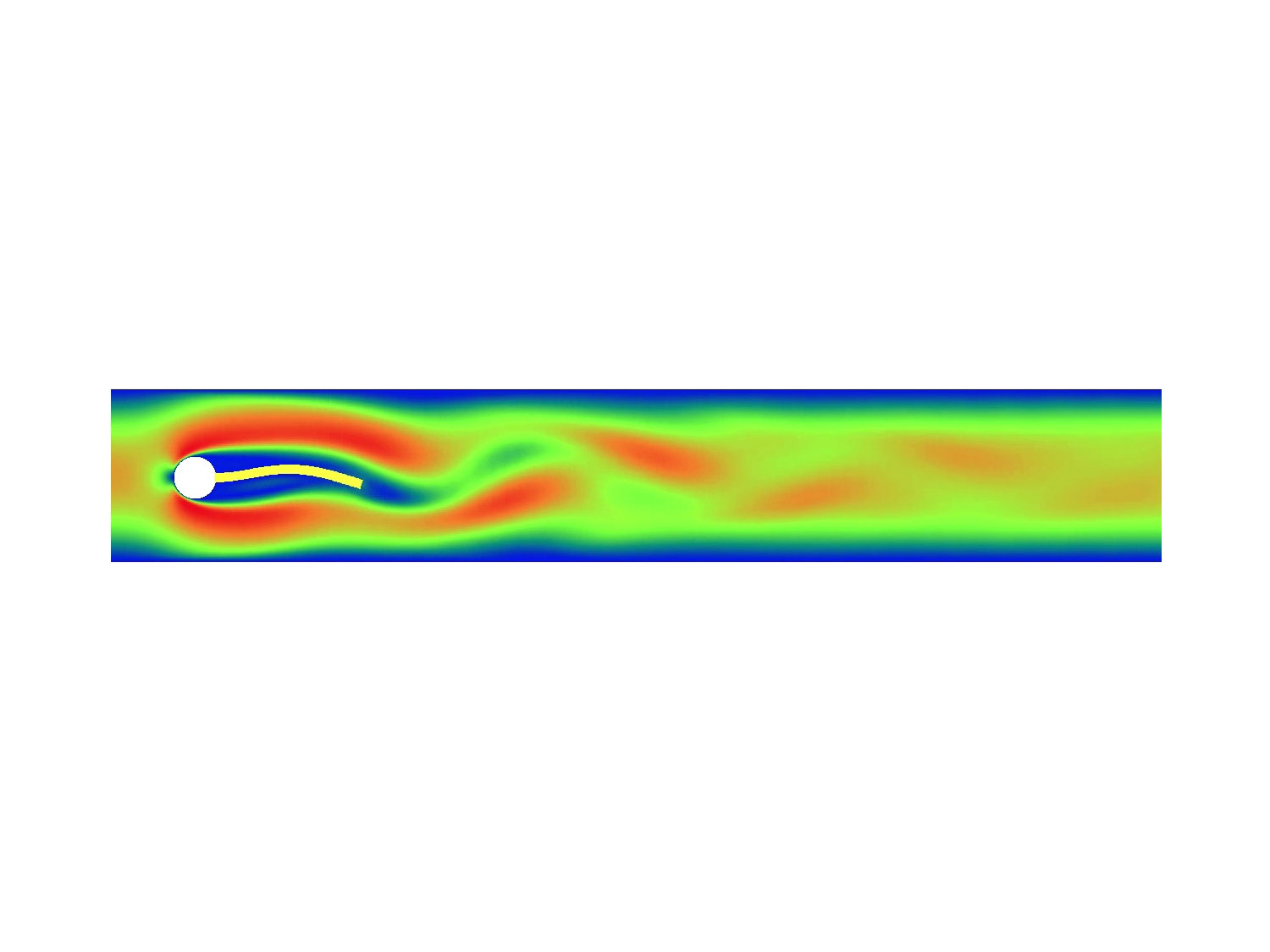
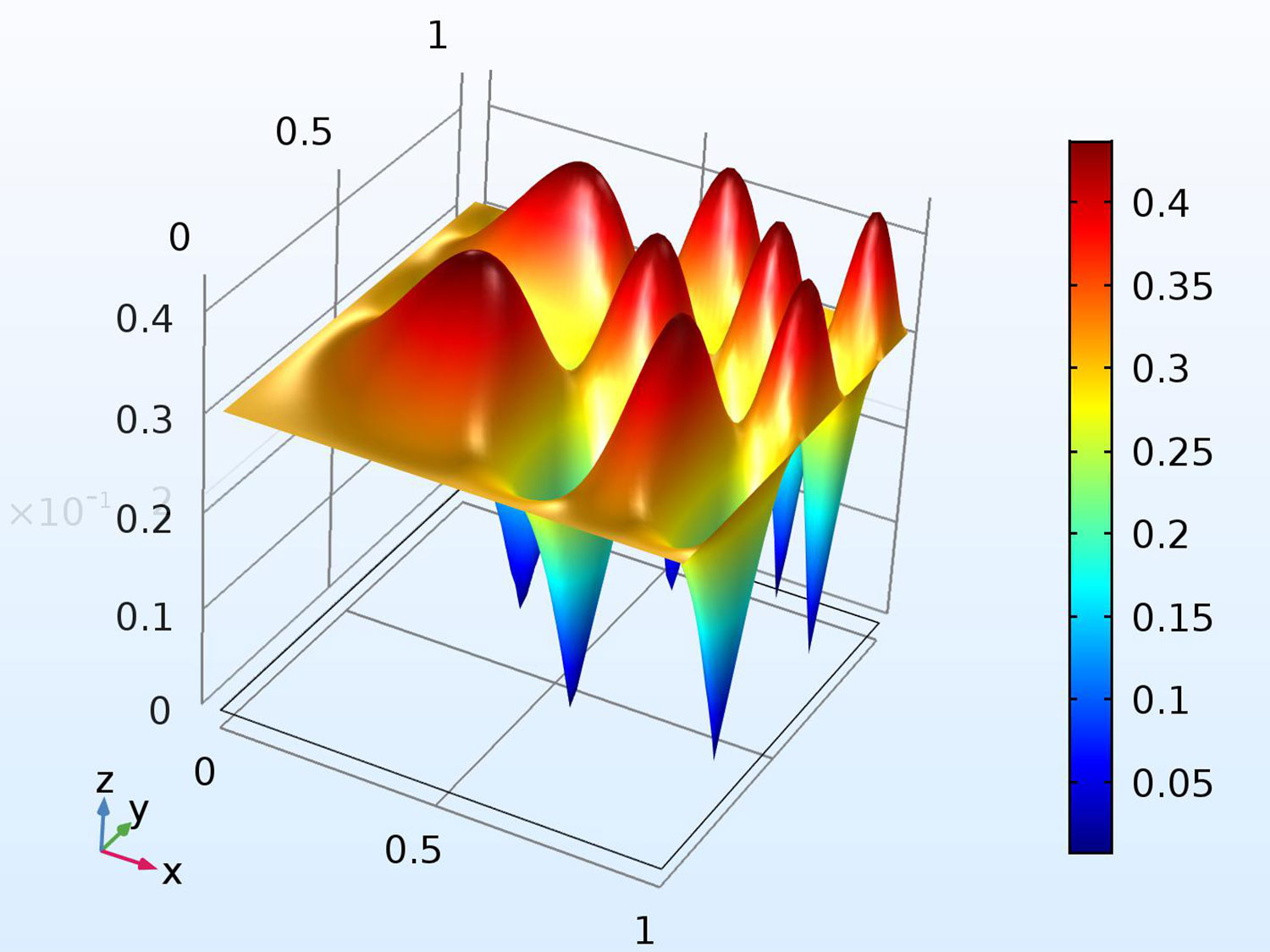
Acoustic Streaming: A Lagrangian– Eulerian Perspective
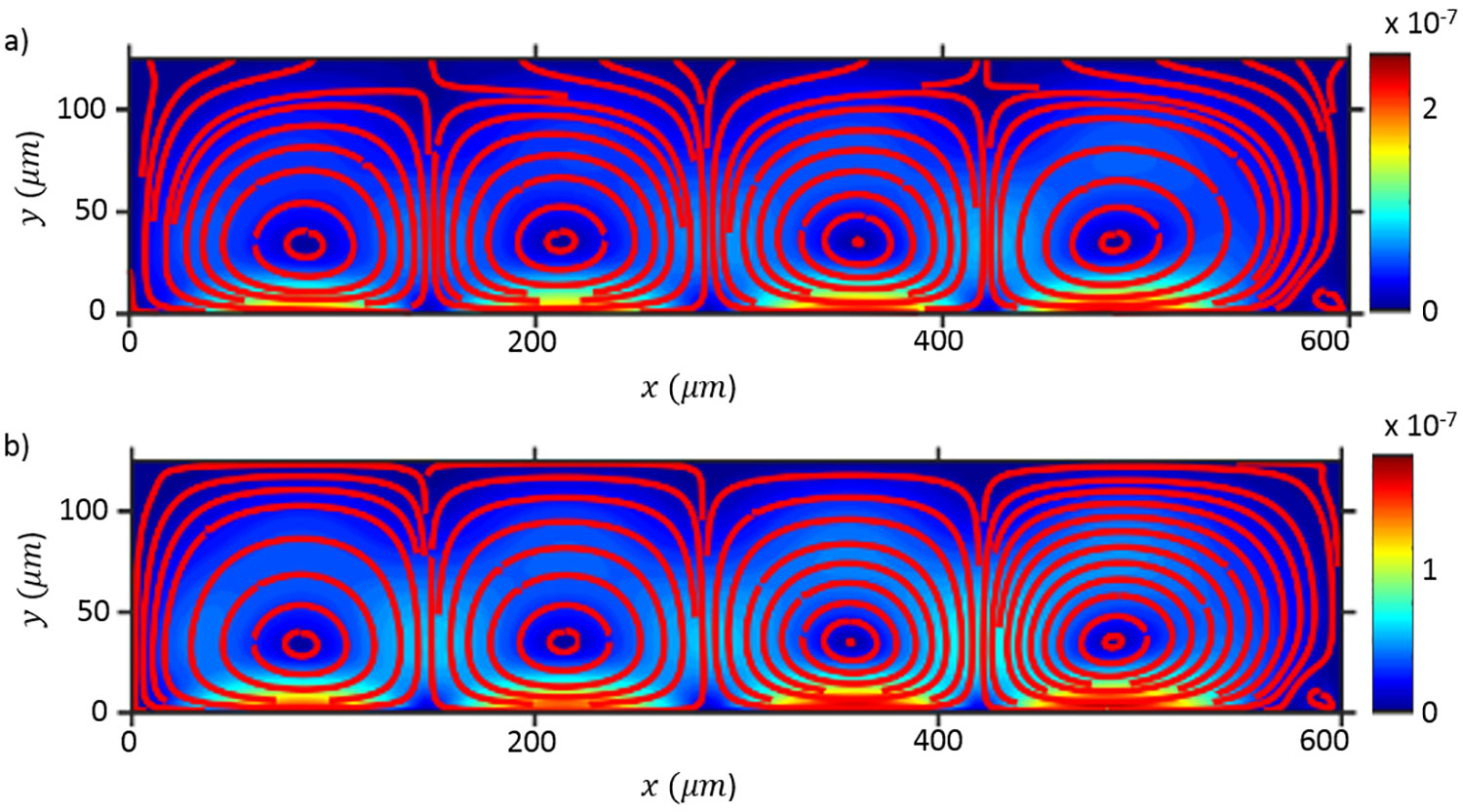
The propagation of acoustic waves in fluids is the basis for a plethora of lab-on-a-chip applica- tions, with the consequent prospect of revolutionizing point-of-care diagnostics in biomedical applications. While there have been many recent reports on the physics in confined reso- nant chamber, the physical understanding of acoustically-driven fluid and particle motion in confined leaky systems is limited. Not only is there a strong need for a mathematical and numerical framework in support of the devices in question, but there is also a need for the identification of “canonical” or benchmark experiments that can be used to validate the the- oretical framework. This paper lays the foundation for the analysis of microacoustofluidics by switching the framing of the problem from its traditional Eulerian view to an arbitrary Lagrangian-Eulerian formulation. This may seem a simple reformulation without modification of the underlying physics and therefore an exercise without much practical merit. However, this is not the case. Theoretical microacoustofluidics is, at its core, a homogenization prob- lems in time. Specifically, it consists in identifying dominant space and time scales and then using asymptotic expansions to create a cascade of boundary-value problems whose orders are defined by the separation of the identified scales. When used in practice, these expansions are truncated so as to consist of only on a finite number of problems. Therefore, the prob- lems generated by di erence kinematic frameworks yields di erent problems. In this paper we argue for the first time that an ALE perspective allows one to provide transparency to the boundary conditions used, the latter being only approximate in Eulerian formulations. In addition, the ALE formulation yields governing equations for the slow streaming that have less stringent regularity requirements compared to those yielded by the Eulerian framework. In very recent work, we have already provided practical results that demonstrated that the ALE formulation of the problems yields qualitative and quantitative results that are much closer to experimental results, so much so that the identification of an experimental bench- mark problem seems now within reach. Furthermore, we have demonstrated improved orders of convergence of the correspondent numerical implementation.† Continuation of this work in ongoing and corresponding publications are under review and in preparation.
Source:
Nama, N., T. J. Huang, and F. Costanzo (2017), “Acoustic Streaming: A Lagrangian– Eulerian Perspective”, Journal of Fluid Mechanics, 825, pp. 600–630,
DOI: 10.1017/jfm.2017.338.
Links to Videos:
https://youtu.be/cKmDjagN77k